树状数组

Binary Indexed Tree

问题描述

首先来引入一个问题：

给定$n$个数字，有两种频繁的操作需要处理：

  • 求$\sum_{k = i}^j A_k$；
  • 对某个$A_i$数据进行增减操作。

如果我们使用普通的数组，这两种操作的复杂度分别为$O(n)$和$O(1)$，如果进行$m$次操作，最坏的情况下，复杂度是$O(mn)$的。

所以，为了降低复杂度，我们可以使用一种数组数组的结构，可以将复杂度降低到$O(m\lg n)$。当然，可以使用$RMQ$的方法，但是$RMQ$的编程实现稍微麻烦些，所以这里介绍数组数组的方法。

算法介绍

问题建模

因为每个整数都能表示为一些2的幂次方的和，类似于海明码的思路，我们可以使用一个数组，每个数组保存一段数字的求和结果。即为数组里面的元素$BIT_i$对于某一段数据“负责”。

那么如何指定划分的方法，使得每个数组元素各司其职，不会导致浪费呢？我们可以通过对应下标转换为二进制以后的数字来进行确定。这里我们根据每个元素最右边的$1$的位置$r$进行判断。指定索引$i$的负责区域是从$i - 2^r + 1$到$i$。如图所示：

那么如何确定最右边$1$的位置？我们借助计算机基础的知识可知：$r = x \& (-x)$。

值得一提的是，树状数组中，我们使得下标从$1$开始，这样可以极大的方便我们编程处理。

那么此时获取从数据开头到结尾的求和就很简单，只要给定了数组的下标，我们就可以了解到是哪些$BIT$里面的数据在储存这些求和，将其相加就好。

同样的修改也是类似的思路，我们只需要知道如果知道了需要修改位置的下标，就可以确定需要修改哪些“负责人”的值。

求解方法

对于求$r$，在C++里可以将其定义为内联函数，方便求解：

1
2
3
inline int lowbit(int x) {
    return x & (-x);
}

如果需要求解从开始到位置$i$这一段的和，通过迭代的方式，可以很方便的找到负责任的节点，进行累加操作：

1
2
3
4
5
6
7
8
int sum(int x) {
    int res = 0;
    while (x > 0) {
        res += BIT[x];
        x -= lowbit(x);
    }
    return res;
}

如果需要更新某一个位置的数据，可以做一个求和的逆运算，从低往上的修改负责位置：

1
2
3
4
5
6
void edit(int x, int delta) {
    while (x < MAXN) {
        BIT[x] += delta;
        x += lowbit(x);
    }
}

在题目的求解过程中，我们经常使用一个求区间$[i, j]$的和的操作，很容易想到，可以通过求$sum(i)$和$sum(j)$以后，直接相减获得。

但是注意到，这里其实是出现了很多的浪费，主要表现为区间$[1, min(i, j)]$中，有相当一部分数据辛辛苦苦求出来以后，又再次相减掉了。其中最坏的情况是只求一个数字，如求$A_i$，这样有$2\times (\ulcorner\log_2i\urcorner + 1)$次求解都被浪费，对于这种情况，是有对应的方法的。但是会增加些代码复杂性，而且在$O()$标记中是系数项，没有本质影响，在此我们可以先忽视它。

解题报告

Poj 3321 Apple Tree

问题描述

There is an apple tree outside of kaka’s house. Every autumn, a lot of apples will grow in the tree. Kaka likes apple very much, so he has been carefully nurturing the big apple tree.

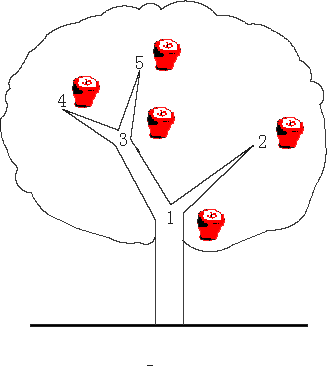
The tree has N forks which are connected by branches. Kaka numbers the forks by 1 to N and the root is always numbered by 1. Apples will grow on the forks and two apple won’t grow on the same fork. kaka wants to know how many apples are there in a sub-tree, for his study of the produce ability of the apple tree.

The trouble is that a new apple may grow on an empty fork some time and kaka may pick an apple from the tree for his dessert. Can you help kaka?

  • Input

    The first line contains an integer N (N ≤ 100,000) , which is the number of the forks in the tree.
    The following N - 1 lines each contain two integers u and v, which means fork u and fork v are connected by a branch.
    The next line contains an integer M (M ≤ 100,000).
    The following M lines each contain a message which is either
    “C x“ which means the existence of the apple on fork x has been changed. i.e. if there is an apple on the fork, then Kaka pick it; otherwise a new apple has grown on the empty fork.
    or
    “Q x“ which means an inquiry for the number of apples in the sub-tree above the fork x, including the apple (if exists) on the fork x
    Note the tree is full of apples at the beginning

  • Output

    For every inquiry, output the correspond answer per line.

算法设计

题目中需要求解的是一个子树上所有苹果的个数，如果我们直接开辟空间维护每个子树，那么不论是空间还是时间都是不可以接受的。考虑到树状数组能够求和的性质，我们记录每个点到根节点的上共有多少的苹果。

但是仅仅维护这个数据是不够的，因为我们并不知道从一个树杈上长出来的苹果总和。所以，需要使用$DFS$对于每个节点进行一个编号，同时，对于每一个分叉节点，记录自己从最小孩子到最大孩子的编号，方便查找。这样我们通过查询一个树杈最大最小儿子分别到根节点的苹果数，将这两者相减就是自己所有孩子的苹果总数。最后再加上自己的苹果，就是需要查询的内容。

注意到，题目只保证了根节点编号为$1$，所以需要自己维护一个映射关系，方便从题目给定的节点映射到按照$DFS$顺序访问的节点。

程序代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int MAXN = 100000 + 10;
int BIT[MAXN];
struct Edge {
    int to;
    int next;
};
struct Map {
    int begin;
    int end;
};
Edge edge[MAXN * 2];
int head[MAXN];
Map idMap[MAXN];
int apple[MAXN];
int cnt;
int id;
inline void addEdge(int u, int v) {
    edge[++cnt].to = v;
    edge[cnt].next = head[u];
    head[u] = cnt;
}
inline int lowbit(int x) {
    return x & (-x);
}
inline int sum(int x) {
    int res = 0;
    while (x > 0) {
        res += BIT[x];
        x -= lowbit(x);
    }
    return res;
}
inline void edit(int x, int delta) {
    while (x < MAXN) {
        BIT[x] += delta;
        x += lowbit(x);
    }
}
void DFS(int u, int father) {
    idMap[u].begin = ++id;
    for (int i = head[u]; i != 0; i = edge[i].next) {
        if (edge[i].to == father)
            continue;
        DFS(edge[i].to, u);
    }
    idMap[u].end = id;
}
int n, i, u, v, m;
char c;
int main () {
    std::ios::sync_with_stdio(false);
#ifdef LOCAL
    freopen("input.txt", "r", stdin);
#endif
    scanf("%d", &n);
    for (i = 0; i < n - 1; ++i) {
        scanf("%d %d", &u, &v);
        addEdge(u, v);
        addEdge(v, u);
    }
    DFS(1, -1);
    for (i = 1; i <= n; ++i) {
        apple[i] = 1;
    }
    for (i = 1; i <= n; ++i) {
        edit(idMap[i].begin, 1);
    }
    scanf("%d", &m);
    while (m--) {
        getchar();
        scanf("%c %d", &c, &u);
        if (c == 'C') {
            if (apple[u]) {
                apple[u] = 0;
                edit(idMap[u].begin, -1);
            }
            else {
                apple[u] = 1;
                edit(idMap[u].begin, 1);
            }
        }
        else {
            printf("%d\n", apple[u] + sum(idMap[u].end) - sum(idMap[u].begin));
        }
    }
}

性能分析

由之前的分析可以知道，每次对于$BIT$的操作复杂度都是$O(\lg n)$，所以，一共是$m$次输入，总共的复杂度为$O(m\lg n)$，对于这个树来说，之前$DFS$的$O(n)$的遍历可以不计。

编程技术技巧

存粹编程的角度来说，此题并没有使用太多的技巧。

不过第一次接触，很难想到求一个子树和的问题，可以转为一个线性数组的求和。相当于通过$DFS$遍历标号以后，将一个二维的结构，转为一个一维的结构进行求解。通过迂回的求出每个点到根的苹果总数，相减后求子树苹果总和的方法十分巧妙。

Poj 1990 MooFest

问题描述

Every year, Farmer John’s N (1 <= N <= 20,000) cows attend “MooFest”,a social gathering of cows from around the world. MooFest involves a variety of events including haybale stacking, fence jumping, pin the tail on the farmer, and of course, mooing. When the cows all stand in line for a particular event, they moo so loudly that the roar is practically deafening. After participating in this event year after year, some of the cows have in fact lost a bit of their hearing.

Each cow i has an associated “hearing” threshold v(i) (in the range 1..20,000). If a cow moos to cow i, she must use a volume of at least v(i) times the distance between the two cows in order to be heard by cow i. If two cows i and j wish to converse, they must speak at a volume level equal to the distance between them times max(v(i),v(j)).

Suppose each of the N cows is standing in a straight line (each cow at some unique x coordinate in the range 1..20,000), and every pair of cows is carrying on a conversation using the smallest possible volume.

Compute the sum of all the volumes produced by all N(N-1)/2 pairs of mooing cows.

  • Input

    Line 1: A single integer, N

    Lines 2..N+1: Two integers: the volume threshold and x coordinate for a cow. Line 2 represents the first cow; line 3 represents the second cow; and so on. No two cows will stand at the same location.

  • Output

    Line 1: A single line with a single integer that is the sum of all the volumes of the conversing cows.

算法设计

这里的树状数组应用比较巧妙，并不是很好想，因为需要输出最小的音量和，我们将牛先按照听力从大到小的顺序排列，优先满足听力差的牛。

这时，需要维护两个树状数组，一个用来求解这头牛$i$坐标之前的牛数，一个用来计算当前的距离和。

这样可以将当前的牛分成两组，一边是坐标在左边的，一边是坐标在右边的。通过距离和听力来求出音量。

程序代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
typedef unsigned long long ull;
const int MAXN = 20000 + 5;
struct Cow {
    int v;
    int x;
};
bool cmp(const Cow &lhs, const Cow &rhs) {
    return lhs.v < rhs.v;
}
Cow cow[MAXN];
ull BITCount[MAXN];
ull BITDistance[MAXN];
int n;
inline int lowbit(int x) {
    return x & (-x);
}
inline ull sum(int x, ull *BIT) {
    ull res = 0;
    while (x > 0) {
        res += BIT[x];
        x -= lowbit(x);
    }
    return res;
}
inline void edit(int x, ull *BIT, ull delta) {
    while (x < MAXN) {
        BIT[x] += delta;
        x += lowbit(x);
    }
}
int main () {
    std::ios::sync_with_stdio(false);
#ifdef LOCAL
    freopen("input.txt", "r", stdin);
#endif
    scanf("%d", &n);
    for (int i = 0; i < n; ++i) {
        scanf("%d %d", &cow[i].v, &cow[i].x);
    }
    sort(cow, cow + n, cmp);
    ull res = 0;
    ull totalDistance = 0;
    for (int i = 0; i < n; ++i) {
        ull leftCount = sum(cow[i].x, BITCount);
        ull leftDistance = sum(cow[i].x, BITDistance);
        res += (ull)cow[i].v * (leftCount * (ull)cow[i].x - leftDistance);
        res += (ull)cow[i].v * (totalDistance - leftDistance - ((ull)i - leftCount) * (ull)cow[i].x);
        totalDistance += (ull)cow[i].x;
        edit(cow[i].x, BITCount, 1);
        edit(cow[i].x, BITDistance, (ull)cow[i].x);
    }
    printf("%llu\n", res);
}

性能分析

这里对于排序和两个树状数组的操作，复杂度都是$O(n\lg n)$，所以最后的复杂度不变。

编程技术技巧

此题其实不容易想到构造两个树状数组进行求解，因为树状数组的性质只对于求和比较方便，所以这里需要一次求和区分坐标，一次求和区分距离。

Poj 2892 Tunnel Warfare

问题描述

During the War of Resistance Against Japan, tunnel warfare was carried out extensively in the vast areas of north China Plain. Generally speaking, villages connected by tunnels lay in a line. Except the two at the ends, every village was directly connected with two neighboring ones.

Frequently the invaders launched attack on some of the villages and destroyed the parts of tunnels in them. The Eighth Route Army commanders requested the latest connection state of the tunnels and villages. If some villages are severely isolated, restoration of connection must be done immediately!

  • Input

    The first line of the input contains two positive integers n and m (n, m ≤ 50,000) indicating the number of villages and events. Each of the next m lines describes an event.

    There are three different events described in different format shown below:

    D x: The x-th village was destroyed.
    Q x: The Army commands requested the number of villages that x-th village was directly or indirectly connected with including itself.
    R: The village destroyed last was rebuilt.

  • Output

    Output the answer to each of the Army commanders’ request in order on a separate line.

算法设计

此题思路比较清晰，因为地道在不断的被破坏，所以需要用一个动态的数组进行维护求和。这里使用了树状数组进行求和。但是我们需要查找从某个点$i$处，左右的连续地道，所以此时需要对数组进行全局的搜索，找到一个满足要求的最长连续区间。

值得一提的是，如果直接暴力搜索，每一次查询的复杂度都是$O(n\lg n)$，最后的复杂度是$O(n^2\lg n)$，比较耗时。这里我们可以使用二分查找的思想，寻找到满足要求的区间值。

最后，这道题目需要进行修复的工作，我们可以通过一个简单的栈结构进行记录。

程序代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
const int MAXN = 50000 + 5;
int BIT[MAXN];
int stack[MAXN];
int tmp[MAXN];
int sp;
int n, m, x;
char input;
inline int lowbit(int x) {
    return x & (-x);
}
inline int sum(int x) {
    int res = 0;
    while (x > 0) {
        res += BIT[x];
        x -= lowbit(x);
    }
    return res;
}
inline void edit(int x, int delta) {
    while (x <= n) {
        BIT[x] += delta;
        x += lowbit(x);
    }
}
int countLeft(int x) {
    int left = 0, right = x;
    int mid;
    int pos = 0;
    while (left <= right) {
        mid = (left + right) >> 1;
        if (sum(x) - sum(mid) == 0) {
            pos = mid;
            right = mid - 1;
        }
        else {
            left = mid + 1;
        }
    }
    return pos;
}
int countRight(int x) {
    int left = x - 1, right = n;
    int mid;
    int pos = 0;
    while (left <= right) {
        mid = (left + right) >> 1;
        if (sum(mid) - sum(x - 1) > 0) {
            right = mid - 1;
        }
        else {
            left = mid + 1;
            pos = mid;
        }
    }
    return pos;
}
int main () {
    std::ios::sync_with_stdio(false);
#ifdef LOCAL
    freopen("input.txt", "r", stdin);
#endif
    scanf("%d %d", &n, &m);
    while (m--) {
        getchar();
        scanf("%c", &input);
        if (input != 'R')
            scanf("%d", &x);
        switch (input) {
            case 'D':
                tmp[x] = 1;
                stack[sp++] = x;
                edit(x, 1);
                break;
            case 'Q':
                if (tmp[x] == 1) {
                    printf("0\n");
                    continue;
                }
                else {
                    printf("%d\n", countRight(x) - countLeft(x));
                }
                break;
            default:
                int pos = stack[--sp];
                tmp[pos] = 0;
                edit(pos, -1);
                break;
        }
    }
}

性能分析

因为这里使用了二分查找进行优化，所以每一次查询工作都是$O(\lg^2n)$的复杂度。最后总的复杂度是$O(n\lg^2n)$。

编程技术技巧

这道题目是使用二分进行优化的一个很巧妙的例子，通过使用二分查找，将$O(n)$次操作降低到了$O(\lg n)$。这就体现了二分的思想是无所不在的。每当我们需要一个搜索操作的时候，都可以考虑能够进行二分的改善。

Poj 2481 Cows

问题描述

Farmer John’s cows have discovered that the clover growing along the ridge of the hill (which we can think of as a one-dimensional number line) in his field is particularly good.

Farmer John has N cows (we number the cows from 1 to N). Each of Farmer John’s N cows has a range of clover that she particularly likes (these ranges might overlap). The ranges are defined by a closed interval [S,E].

But some cows are strong and some are weak. Given two cows: cowi and cowj, their favourite clover range is [Si, Ei] and [Sj, Ej]. If Si <= Sj and Ej <= Ei and Ei - Si > Ej - Sj, we say that cowiis stronger than cowj.

For each cow, how many cows are stronger than her? Farmer John needs your help!

  • Input

    The input contains multiple test cases.
    For each test case, the first line is an integer N (1 <= N <= 10^5), which is the number of cows. Then come N lines, the i-th of which contains two integers: S and E(0 <= S < E <= 10^5) specifying the start end location respectively of a range preferred by some cow. Locations are given as distance from the start of the ridge.

    The end of the input contains a single 0.

  • Output

    For each test case, output one line containing n space-separated integers, the i-th of which specifying the number of cows that are stronger than cowi.

算法设计

题目比较基础，唯一需要进行改进的地方在于，需要对于输入的区间进行排序操作。

因为要统计活动范围能够覆盖其他牛的强壮牛的个数，所以将牛的活动区间按照左端点进行从小到大的排序，如果遇到了左端点相同的情况，需要对于右端点进行从大到小的排序。

这样，在对于排好序的区间进行遍历的时候，只要计算范围内的点的总数就好。

不过，如果有重合的情况，我们还需要通过保存一个过程手动进行处理。

最后，只需要将之前的数据正向的恢复，按照输入的顺序再次排序，即可完成。

程序代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int MAXN = 100000 + 10;
int BIT[MAXN];
inline int lowbit(int x) {
    return x & (-x);
}
inline int sum(int x) {
    int res = 0;
    while (x > 0) {
        res += BIT[x];
        x -= lowbit(x);
    }
    return res;
}
inline void edit(int x, int delta) {
    while (x < MAXN) {
        BIT[x] += delta;
        x += lowbit(x);
    }
}
struct CowRange {
    int x;
    int y;
    int index;
    int res;
    CowRange(): x(0), y(0), index(0), res(0) {}
    CowRange(int x, int y, int index): x(x), y(y), index(index), res(0) {}
};
bool preHandle(const CowRange& lhs, const CowRange& rhs) {
    return lhs.x < rhs.x || ((lhs.x == rhs.x) && (lhs.y > rhs.y));
}
bool finishHandle(const CowRange& lhs, const CowRange& rhs) {
    return lhs.index < rhs.index;
}
CowRange cows[MAXN];
int n;
int cnt;
int main () {
    std::ios::sync_with_stdio(false);
#ifdef LOCAL
    freopen("input.txt", "r", stdin);
#endif
    while (scanf("%d", &n) == 1 && n) {
        int x, y;
        memset(BIT, 0, sizeof(BIT));
        cnt = 0;
        while (cnt < n) {
            scanf("%d %d", &x, &y);
            CowRange &r = cows[cnt++];
            r.x = x;
            r.y = y;
            r.index = cnt;
        }
        int pointCnt = 0, saveCnt = 0;
        sort(cows, cows + cnt, preHandle);
        for (int i = 0; i < cnt; ++i) {
            if (i != 0 && cows[i].y == cows[i - 1].y && cows[i].x == cows[i - 1].x){
                cows[i].res = saveCnt;
            }
            else {
                int aeCnt = pointCnt - sum(cows[i].y + 1);
                cows[i].res = aeCnt;
                saveCnt = aeCnt;
            }
            ++pointCnt;
            edit(cows[i].y + 2, 1);
        }
        sort(cows, cows + cnt, finishHandle);
        for (int i = 0; i < cnt - 1; ++i) {
            printf("%d ", cows[i].res);
        }
        printf("%d\n", cows[cnt - 1].res);
    }
}

性能分析

这里对于树状数组和排序操作的复杂度相同，全都为$O(n\lg n)$。

编程技术技巧

因为题目和前面$3$题都很像，思想也基本类似，所以技巧可以参考前面的题目。

扫一扫，分享到微信

微信分享二维码

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

现就读于华中科技大学<br><br>2018加油<br><br>做咸鱼也要做最咸的一条<br>